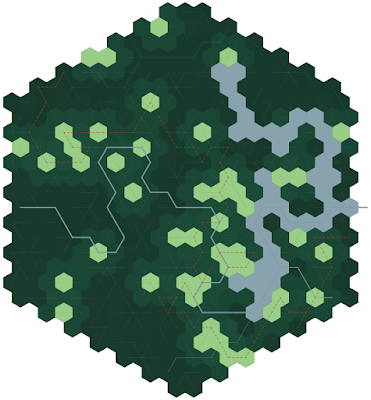
Adding lakes was easy once I decided that I wasn't going to approach the beautiful detail of Undiscovered Worlds. All I need is a representation of a concept (which, at its heart, is the essence of a map anyway).
Low-quality lakes are easy to make. All I do is find where two rivers meet, then expand the lake around that point, flowing into any lower hexes. Usually, this means I end up with lots of long "lakes" which simply follow the river. This is a side effect of the terrain generation.
Still, small inconsistencies in the system are outweighed by its usefulness (and can always be addressed later). I can search over my 20-hex world map, find a place that looks interesting, and generate it quickly in detail.
One thing that inevitably comes to mind is just how much of this country is wild...but at the same time, there are a good number of scattered villages. How much conflict happens here between the humanoids and their encroaching civilization and the intelligent creatures who want to stay put? A good deal, I'll reckon. Not to mention, with a couple good scouts in your party, you might be able to hide from the law here for years. That's a lot of area to search.
I do have plans to implement a suggestion from Scott and blend the terrain edges together more smoothly.
Now if only I could get a proper SVG to PNG export...Inkscape is ok for some things but my installation has proved miserable when it comes to applying filters and blends.
June 26, 2019
June 21, 2019
History XV: A Feebleness Bereft of Breeding
There remain a few mechanics to topple empires that I haven't yet tackled. The next one on the list is the Plague.
For now, "plague" is intentionally vague. In modern parlance, the term generally refers to the three kinds of disease spread by the Yersinia pestis bacterium: bubonic, septicemic, and pnuemonic plagues. The properties of each are different, so for now I want to think about a general model for plague transmission of infectious diseases. Diseases which may cause epidemics but are not usually transmitted infectiously, such as cholera, are also interesting but can be tackled separately.
Alexis addresses some initial thoughts about a player catching disease (or building up a town's resistance to such) here. As a town's infrastructure rises, the individual's chance for becoming diseased grows, to the tune of $I \ over 10000$. For a settlement of $I = 474$, the chance would then be $0.0474\%$. That's not so bad. In addition, this is just "disease." That's pretty broad. Let's place the chance of contracting actual plague at 0.2%, on top of the chance to contract any disease. That makes the overall chance really low, 0.009%.
Like anything else you might care to learn about, the amount of research done on the subject is staggering. Consider these sources:
For now, "plague" is intentionally vague. In modern parlance, the term generally refers to the three kinds of disease spread by the Yersinia pestis bacterium: bubonic, septicemic, and pnuemonic plagues. The properties of each are different, so for now I want to think about a general model for plague transmission of infectious diseases. Diseases which may cause epidemics but are not usually transmitted infectiously, such as cholera, are also interesting but can be tackled separately.
Alexis addresses some initial thoughts about a player catching disease (or building up a town's resistance to such) here. As a town's infrastructure rises, the individual's chance for becoming diseased grows, to the tune of $I \ over 10000$. For a settlement of $I = 474$, the chance would then be $0.0474\%$. That's not so bad. In addition, this is just "disease." That's pretty broad. Let's place the chance of contracting actual plague at 0.2%, on top of the chance to contract any disease. That makes the overall chance really low, 0.009%.
Like anything else you might care to learn about, the amount of research done on the subject is staggering. Consider these sources:
- Math behind the Infection
- Modeling plague transmission inMedieval European cities
- The mathematics of disease
Even from just these, a clearer picture emerges of how to model such an event. Particularly, a set of equations (the SIR model), which always interests me. \[{\partial S \over \partial t} = B - {\beta S I \over N} - d S\]\[{\partial I \over \partial t} = {\beta S I \over N} - \gamma I - d I\]\[{\partial R \over \partial t} = \gamma m I - d R\], where $S$ is the susceptible population, $I$ is the infected population, $R$ is the recovered population, $N = S + I + R$ is the total population, $B = 0.4$ is the birth rate, $\beta=0.5$ is the contact rate, $d=0.4$ is the death rate, ${1 \over \gamma} = 26$ is the infectious period, and $m=0.33$ is the mortality. By tweaking these parameters (this particular set is for bubonic plague) we can model different kinds of diseases when we wish.
I don't really care about $B$ and $d$ since these time steps are usually modeled in days and I step history forward one year at a time. So all the calculation will take place in a single fell swoop. \[{\partial S \over \partial t} = -{\beta S I \over N}\]\[{\partial I \over \partial t} = {\beta S I \over N} - \gamma I\]\[{\partial R \over \partial t} = \gamma m I\]. This generates a curve that's quite nice when modeled with the above parameters, for a city that begins with a population of 32,210 and a single infection:
That's pretty devastating.
The plague then spreads to a neighboring city, which must make its own save against infection. And the cycle repeats. A city could shake off the plague but then get it again from a neighbor. This makes a death spiral possible to wipe out an entire civilization.
....Now having done all this work, it occurs to me that the fancy equations are irrelevant. The only way to be removed from the pool entirely is to die...which means that the only calculation necessary is $N_1 = \mu N_0$. Huh. However, the full calculation can still tell me how long the epidemic lasts, in order to spread it to other settlements over more than one year. Plus, it might be interesting to know how many total are infected in case the party is caught in the middle of an epidemic.
Somewhat anticlimatic.
....Now having done all this work, it occurs to me that the fancy equations are irrelevant. The only way to be removed from the pool entirely is to die...which means that the only calculation necessary is $N_1 = \mu N_0$. Huh. However, the full calculation can still tell me how long the epidemic lasts, in order to spread it to other settlements over more than one year. Plus, it might be interesting to know how many total are infected in case the party is caught in the middle of an epidemic.
Somewhat anticlimatic.
June 19, 2019
Detail V | Roads VIII
Roads are easier than rivers because they do not shape the terrain they "flow" through as rivers do. I thought they would be more complicated but they turned out to be quite simple.
The river ingress and egress hexes are found by doing a transform on the character values of the strings of the names of the hexes. This gives a nice stochastic but repeatable location. For the roads, I simply reverse the inputs. Badabingbadaboom.
The roads (which are defined at the 20-hex level) enter the hex and make their way to the 1-hex with the highest infrastructure, which is located on the river and is assumed to be the settlement center. Where there are no roads, there are trails. Trails may or may not be well maintained, and they are not suitable for significant trade. But they allow transportation of goods and supplies to and from remote outposts such as mines which may not have access to a main trade road. Again, these trails all seek the assumed central hex.
Trails are also defined at the 20-hex level to connect settlements with low infrastructures. Generally speaking, a road will only occur through a 20-hex with $I\geq 50$. An exception is made if the road is being laid (and maintained) from capital to capital. Therefore, trails are used instead to connect lower $I$ settlements as well as provide access to hinterlands.
As a note on the trade system: only 20-hexes with a road can have a market. If your settlement has no market, you'll have to travel to find one. All goods produced in a 20-hex without a market must find their way down a trail to somewhere they can be sold. Therefore, for the purposes of the system, these goods are credited as being produced in the market settlement, even though their physical location might be different. My trade system engine assigns them to the market which is closest in the network.
This raises interesting gameplay situations. Most people in these remote locations would either make their own tools or carefully guard something they took a specific trip to buy. Very rarely would a merchant make their way down these dangerous and unfriendly trails to sell their wares. Plan accordingly.
The river ingress and egress hexes are found by doing a transform on the character values of the strings of the names of the hexes. This gives a nice stochastic but repeatable location. For the roads, I simply reverse the inputs. Badabingbadaboom.
The roads (which are defined at the 20-hex level) enter the hex and make their way to the 1-hex with the highest infrastructure, which is located on the river and is assumed to be the settlement center. Where there are no roads, there are trails. Trails may or may not be well maintained, and they are not suitable for significant trade. But they allow transportation of goods and supplies to and from remote outposts such as mines which may not have access to a main trade road. Again, these trails all seek the assumed central hex.
Trails are also defined at the 20-hex level to connect settlements with low infrastructures. Generally speaking, a road will only occur through a 20-hex with $I\geq 50$. An exception is made if the road is being laid (and maintained) from capital to capital. Therefore, trails are used instead to connect lower $I$ settlements as well as provide access to hinterlands.
 |
| Darker hexes are less civilized, road in red |
As a note on the trade system: only 20-hexes with a road can have a market. If your settlement has no market, you'll have to travel to find one. All goods produced in a 20-hex without a market must find their way down a trail to somewhere they can be sold. Therefore, for the purposes of the system, these goods are credited as being produced in the market settlement, even though their physical location might be different. My trade system engine assigns them to the market which is closest in the network.
This raises interesting gameplay situations. Most people in these remote locations would either make their own tools or carefully guard something they took a specific trip to buy. Very rarely would a merchant make their way down these dangerous and unfriendly trails to sell their wares. Plan accordingly.
June 18, 2019
History XVI: God Gave a Loaf to Every Bird
The famine mechanic is killing city development. As it should! However, it's too much. Nothing can develop past a few thousand people. Since rural population is dependent on infrastructure, neither can ever increase to the point where actual substantial growth is possible. And that's with a very generous assumption that it only takes 2-3 farmers to feed one urban dweller. Some estimates put this as high as 9.
We want a situation where some settlements can grow and others die out, or where a settlement can be cut off in time of war.
As a "temporary" stop-gap, I've increased the population density significantly in rural areas. This gives you more food-producers. However, starvation still does restrict nation formation. I haven't found a case yet where starvation will completely wipe out a civilization, but it proves significant in politics in the following ways:
Starvation naturally reduces hegemony morale. It can affect it so much that when a larger nation comes knocking on the door, the food-restrained nation acquiesces without a fight. But this in turn can cause problems for the conquerors, who have possibly bitten off more than they can chew.
In addition, hegemonies with very low morale (but no war) are much more likely to experience secession, as cities with large enough infrastructure may feel they're better off striking out on their own. They may or may not be correct.
All of this makes for a complex interplay of resources and politics.
It is very interesting how, watching lines grow in a text file, how I tend to anthropomorphize these collections of bits. I feel national pride swell when a city throws off the yoke of an oppressor, or defeats a stronger neighbor. Let's tell a story.
Menesesese was an elven city founded in 645, in a jungle climate. They named their new civilization Menese. Although they would experience a few major disasters over the years (in 857, 1289, and 1401), they lived in peace with their older neighbor, another elven city called Moterure, which had been founded in 24, six centuries before. By 1543, Mote had founded 8 more cities down the coastline, stretching down to Menesesese.
However, in 1613, Mote attacked and defeated Menesesese, incorporating it into their growing kingdom. This would last until 2185, when Menesesese rebelled, forming the Menesesese hegemony again (I need to add some code so the rebellious hegemon will take its original name, Menese, not the name of the city, which may have prefixes or suffixes as it does in this case).
From 2195-2198, Mote and Menesesese would fight over the cities of Ritikerure, Chorcliste, Mieprure, Wenafrure, Interure, Chorvetek, and Chordmose. Unfortunately, Chrovetek was totally destroyed during the First Mote-Menesesese War. Although Moterure itself did not fall, nearly all its cities now lay in the hands of the Menesesese...-ese. Mote would starve and shrink over the next 50 years.
In 2258, relations again deteriorated, but this time Moterure was more than willing to accept Menesesese rule. Alas, this peace too was not to last, as Mote would rebel only nine years later in 2267, taking with them the cities of Magirure, Neferirure, Savcerure, and Raprurure.
Over the next 1600 years, this story would play out again and again. Cities were destroyed and castles built. As I write this, the simulation is in year 3950. The Twelfth Moterure-Menesesese War ended in 3882. And it surely will not be the last.
This provides me a rich tapestry for a game set around this region. There is plenty of wilderness space, but even the loosely populated landscape is dotted with ruins, reminders of the hatred between these two nations that spans three millennia. I know where all the battles were fought (and where great generals might have fallen and grand items lost), where the ruined cities are located (and where the ghosts of the slain still wander). There are old elves who still fought in the last war...there is peace now, but for how long, they ask? Never trust a Mote. You better be careful not to look too Menesesese in the Neferirure market.
And all of it out of whole cloth.
We want a situation where some settlements can grow and others die out, or where a settlement can be cut off in time of war.
As a "temporary" stop-gap, I've increased the population density significantly in rural areas. This gives you more food-producers. However, starvation still does restrict nation formation. I haven't found a case yet where starvation will completely wipe out a civilization, but it proves significant in politics in the following ways:
Starvation naturally reduces hegemony morale. It can affect it so much that when a larger nation comes knocking on the door, the food-restrained nation acquiesces without a fight. But this in turn can cause problems for the conquerors, who have possibly bitten off more than they can chew.
In addition, hegemonies with very low morale (but no war) are much more likely to experience secession, as cities with large enough infrastructure may feel they're better off striking out on their own. They may or may not be correct.
All of this makes for a complex interplay of resources and politics.
It is very interesting how, watching lines grow in a text file, how I tend to anthropomorphize these collections of bits. I feel national pride swell when a city throws off the yoke of an oppressor, or defeats a stronger neighbor. Let's tell a story.
Menesesese was an elven city founded in 645, in a jungle climate. They named their new civilization Menese. Although they would experience a few major disasters over the years (in 857, 1289, and 1401), they lived in peace with their older neighbor, another elven city called Moterure, which had been founded in 24, six centuries before. By 1543, Mote had founded 8 more cities down the coastline, stretching down to Menesesese.
However, in 1613, Mote attacked and defeated Menesesese, incorporating it into their growing kingdom. This would last until 2185, when Menesesese rebelled, forming the Menesesese hegemony again (I need to add some code so the rebellious hegemon will take its original name, Menese, not the name of the city, which may have prefixes or suffixes as it does in this case).
From 2195-2198, Mote and Menesesese would fight over the cities of Ritikerure, Chorcliste, Mieprure, Wenafrure, Interure, Chorvetek, and Chordmose. Unfortunately, Chrovetek was totally destroyed during the First Mote-Menesesese War. Although Moterure itself did not fall, nearly all its cities now lay in the hands of the Menesesese...-ese. Mote would starve and shrink over the next 50 years.
In 2258, relations again deteriorated, but this time Moterure was more than willing to accept Menesesese rule. Alas, this peace too was not to last, as Mote would rebel only nine years later in 2267, taking with them the cities of Magirure, Neferirure, Savcerure, and Raprurure.
Over the next 1600 years, this story would play out again and again. Cities were destroyed and castles built. As I write this, the simulation is in year 3950. The Twelfth Moterure-Menesesese War ended in 3882. And it surely will not be the last.
This provides me a rich tapestry for a game set around this region. There is plenty of wilderness space, but even the loosely populated landscape is dotted with ruins, reminders of the hatred between these two nations that spans three millennia. I know where all the battles were fought (and where great generals might have fallen and grand items lost), where the ruined cities are located (and where the ghosts of the slain still wander). There are old elves who still fought in the last war...there is peace now, but for how long, they ask? Never trust a Mote. You better be careful not to look too Menesesese in the Neferirure market.
And all of it out of whole cloth.
June 12, 2019
History XV: It Might Be Famine All Around
A hegemony's capital (or largest cities) should be limited by the amount of people they control (hence the working classes ability to keep them supplied).
Currently, this is limited by the carrying capacity, $K$. Therefore, the upper bound on $K$ will be affected by this control.
Assume that $P$ is the population of a city. The farmer ratio $\alpha=3$ can be defined in this case as 3 farmers necessary to support 1 other individual. I'm leaving this as a variable, not a hardcode, because this number is very dependent on who you ask and what time period we're talking about. Therefore, the number of people required to support a city of population $P$ is \[n = \alpha P\]. How many people do we have available? Assuming 100% of the rural population is involved in food production (a bad assumption, again something we can change), then we just need the total amount of rural people in that hegemon $P_r$. How many of those are available to send their goods to our city? If the total urban population of the hegemon is $P_u$, then our city will demand \[{P \over P_u}\] of the resources. This means that only \[{P P_r \over P_u}\] are specifically available to it. We can compare this number to the needed number $n$, and see that \[K_n = \min\left(K, {P P_r \over \alpha P_u}\right)\], that is, if there is enough manual labor, then the city can realize its full potential.
I grabbed a random capital to use for this, Chivenkare. Chivnekare has a population of $P=49920$, and $K\sim55000$. So it is a good test case. It has a good number of cities spread over a large island. Givne this, $n = 149760$. We find that $P_r = 177865$. Already we see danger signs, as Chivenkare is not the only city in its hegemon. However, $P_u = 85887$, so ${P \over P_u} = 0.58$, there may be hope yet.
Ultimately, we find that $K_n = 34460$, meaning that a huge famine is imminent. Sorry, fellas!
This implies a few things for the overall simulation:
Currently, this is limited by the carrying capacity, $K$. Therefore, the upper bound on $K$ will be affected by this control.
Assume that $P$ is the population of a city. The farmer ratio $\alpha=3$ can be defined in this case as 3 farmers necessary to support 1 other individual. I'm leaving this as a variable, not a hardcode, because this number is very dependent on who you ask and what time period we're talking about. Therefore, the number of people required to support a city of population $P$ is \[n = \alpha P\]. How many people do we have available? Assuming 100% of the rural population is involved in food production (a bad assumption, again something we can change), then we just need the total amount of rural people in that hegemon $P_r$. How many of those are available to send their goods to our city? If the total urban population of the hegemon is $P_u$, then our city will demand \[{P \over P_u}\] of the resources. This means that only \[{P P_r \over P_u}\] are specifically available to it. We can compare this number to the needed number $n$, and see that \[K_n = \min\left(K, {P P_r \over \alpha P_u}\right)\], that is, if there is enough manual labor, then the city can realize its full potential.
I grabbed a random capital to use for this, Chivenkare. Chivnekare has a population of $P=49920$, and $K\sim55000$. So it is a good test case. It has a good number of cities spread over a large island. Givne this, $n = 149760$. We find that $P_r = 177865$. Already we see danger signs, as Chivenkare is not the only city in its hegemon. However, $P_u = 85887$, so ${P \over P_u} = 0.58$, there may be hope yet.
Ultimately, we find that $K_n = 34460$, meaning that a huge famine is imminent. Sorry, fellas!
This implies a few things for the overall simulation:
- Cities cut off from the major area of the hegemon will starve and collapse. This is true regardless of the diplomatic relations with the hegemon which surrounds it. Resources are scarce.
- Hegemons at war could collapse very quickly as food runs out, even if they are technically winning overall. This would be a cascading collapse.
- Another cascade could be precipitated by an unrelated catastrophic event.
- Land will be a premium. My automata are not "smart," because they will not seek more land; but those unable to acquire it, spreading influence, infrastructure, and gaining rural working hands, will quickly perish. This mirrors the historical expansion and collapse of many empires, which outgrew their ability to feed themselves and were destroyed in short order.
June 11, 2019
Detail IV: Wilderness Colors
I've just been using a dark and light green to indicate wild and settled terrain. But I need to match that to the actual terrain colors from the 20-hex map.
I really like Welsh Piper's hex generation mechanism so I'll be borrowing some thoughts from here. For now, I'll just define a primary type, a secondary type, and a settled type.
Sometimes, settled will be the same color as unsettled. For example, the halflings, who live in icy terrain, wouldn't be able to grow cropland. In this case, I'll define something like settled = primary, where ice is primary and rock is secondary. So the settled areas are still delineated.
However, most of my test cases right now are in forested areas, so I'll concentrate on those. All those areas turn into grassland type when settled, at least in terms of display. I've also put a pattern over the wild 1-hexes to visually differentiate them if the secondary type is also grassland.
I also implemented a condition where the highest infrastructure hex must be on a river. This ensures that a settlement (when I get around to placing them) will always have access to the river.
Speaking of rivers and colors, I'm not sure the river stands out enough. I also kind of want to make the river a bit more fractalized, but I remember that I'm making a representation, a symbolic map, not a literal terrain map.
It does seem that the heightmap (which is shown by lightning the hex the higher you go) is almost invisible. That's fine; it'll mostly be important for determining the rivers and roads.
To do: roads, coastal 20-hexes, and river sources.
I really like Welsh Piper's hex generation mechanism so I'll be borrowing some thoughts from here. For now, I'll just define a primary type, a secondary type, and a settled type.
Sometimes, settled will be the same color as unsettled. For example, the halflings, who live in icy terrain, wouldn't be able to grow cropland. In this case, I'll define something like settled = primary, where ice is primary and rock is secondary. So the settled areas are still delineated.
However, most of my test cases right now are in forested areas, so I'll concentrate on those. All those areas turn into grassland type when settled, at least in terms of display. I've also put a pattern over the wild 1-hexes to visually differentiate them if the secondary type is also grassland.
 |
| Blitpsy, population 4976, infrastructure 84 |
I also implemented a condition where the highest infrastructure hex must be on a river. This ensures that a settlement (when I get around to placing them) will always have access to the river.
 | |
|
Speaking of rivers and colors, I'm not sure the river stands out enough. I also kind of want to make the river a bit more fractalized, but I remember that I'm making a representation, a symbolic map, not a literal terrain map.
It does seem that the heightmap (which is shown by lightning the hex the higher you go) is almost invisible. That's fine; it'll mostly be important for determining the rivers and roads.
To do: roads, coastal 20-hexes, and river sources.
June 10, 2019
Detail III: Infrastructure
I have been thinking more about how to generate infrastructure for the detailed hexes. I've floated a few ideas here and there which seem to work well, but I thought of an interesting situation where the current system might give odd results.
To sum up, the infrastructure number of a 20-mile hex will indicate how many of the 400 1-mile hexes will be settled. For ease of experiment, let's assume that the 20-hex is forested, and that the settled 1-hexes are cleared land (whether for grazing animals or for houses, doesn't matter yet).
Previously, I was just using the infrastructure number as the number of settled 1-hexes, up to a maximum of 400, at which point the hex would be totally settled. But after reading this post several more times, I believe I can come up with a more robust system.
The problem is that infrastructure spread stops at the boundaries of a hegemony. This means there is a possibility of a hard edge where there is a totally settled 20-hex ($I\geq 400$) next to a relatively unsettled 20-hex (say, $I=10$). The whole point of the detailed 1-hex view is to give a smooth interpolation between discrete 20-hexes.
The Tao (Alexis) uses 2-mile or 6-mile hexes, allowing a smoother interpolation because the detail is not as fine. With the 1-hex, there are 400 hexes that must be made to play nice. He gives a chart, however, detailing the behavior of each hex type and group depending on the number of wilderness hexes that surround it. 2-hexes which are completely settled (Type I) contribute 64 points of infrastructure to the total, and so on down the line. Read the links for more info, I won't rehash it here.
Since I'm not dealing with hex groups directly, I need a way to translate or spring-board off this existing system of ideas into my own map. I will define groups of 1-hexes in the following way: counting the 1-hex itself and the surrounding 6 hexes, how many are wild (of the 7 total)? This gives us 8 total types. Furthermore (and here's the distinctive key): these groups are not discrete. Each hex contributes not only to its own group type, but also those of its neighbors. In this way, the combinations are made even more unique...if it works.
This has some interesting implications. Observe the minimum situation for a Type I hex:
The very presence of the Type I implies a further 6 Type IVs. That's a total of 31, if the above values are used.
Type II (total 24):
Type III (from here on out, I've tried to show the lowest configuration, there are others that could be higher, total 17):
Type IV (total 12):
Type V (total 7):
Type VI (total 4):
Type VII (total 1):
So how do I make this work? I'll start with a brute force approach.
It's very quick to run an algorithm over the 20-hex and get the total infrastructure number based on the 1-hexes. So what I'll do is gradually increase the number of settled 1-hexes and check the number. When I reach the target number, I'm done.
So far, this works pretty well.
Let's try it out for a stark difference. The top hex has $I=1000$, and the bottom two, $I=10$.
Not bad! The edge is still pretty hard...but not as hard. Furthermore, the individual hex groups could be identified for feature placement.
An issue with the infrastructure values for each hex type: The higher the numbers go, the fewer 1-hexes will end up on the final map. Earlier, I had defined 400 as the value of a filled 20-hex: but with the new system, a 20-hex must have $I=2268$. That's pretty high. But it does imply 346 sq. mi. of continuously occupied land (including farmland).
Finally, each iteration is totally random. I want a way to save them so if I come back later, or make a map for a game, I can reproduce it. Each configuration is extremely unique, and so I need a fingerprint. There are a couple of ways I can do it, but here's a very simple one.
First, I sort the hexes by their address, then assign 1 for settled and 0 for wilderness. Then I join all those numbers into a long binary string, padded to 400 zeros. For $I=1000$, that looks like this:
To sum up, the infrastructure number of a 20-mile hex will indicate how many of the 400 1-mile hexes will be settled. For ease of experiment, let's assume that the 20-hex is forested, and that the settled 1-hexes are cleared land (whether for grazing animals or for houses, doesn't matter yet).
Previously, I was just using the infrastructure number as the number of settled 1-hexes, up to a maximum of 400, at which point the hex would be totally settled. But after reading this post several more times, I believe I can come up with a more robust system.
The problem is that infrastructure spread stops at the boundaries of a hegemony. This means there is a possibility of a hard edge where there is a totally settled 20-hex ($I\geq 400$) next to a relatively unsettled 20-hex (say, $I=10$). The whole point of the detailed 1-hex view is to give a smooth interpolation between discrete 20-hexes.
 |
| So what's the point? |
Since I'm not dealing with hex groups directly, I need a way to translate or spring-board off this existing system of ideas into my own map. I will define groups of 1-hexes in the following way: counting the 1-hex itself and the surrounding 6 hexes, how many are wild (of the 7 total)? This gives us 8 total types. Furthermore (and here's the distinctive key): these groups are not discrete. Each hex contributes not only to its own group type, but also those of its neighbors. In this way, the combinations are made even more unique...if it works.
| Type | Adjacent Settled | Infrastructure |
|---|---|---|
| I | 7 | 7 |
| II | 6 | 6 |
| III | 5 | 5 |
| IV | 4 | 4 |
| V | 3 | 3 |
| VI | 2 | 2 |
| VII | 1 | 1 |
| VIII | 0 | 0 |
This has some interesting implications. Observe the minimum situation for a Type I hex:
The very presence of the Type I implies a further 6 Type IVs. That's a total of 31, if the above values are used.
Type II (total 24):
Type IV (total 12):
Type V (total 7):
Type VII (total 1):
So how do I make this work? I'll start with a brute force approach.
It's very quick to run an algorithm over the 20-hex and get the total infrastructure number based on the 1-hexes. So what I'll do is gradually increase the number of settled 1-hexes and check the number. When I reach the target number, I'm done.
So far, this works pretty well.
 |
| $I=113$ |
Not bad! The edge is still pretty hard...but not as hard. Furthermore, the individual hex groups could be identified for feature placement.
An issue with the infrastructure values for each hex type: The higher the numbers go, the fewer 1-hexes will end up on the final map. Earlier, I had defined 400 as the value of a filled 20-hex: but with the new system, a 20-hex must have $I=2268$. That's pretty high. But it does imply 346 sq. mi. of continuously occupied land (including farmland).
Finally, each iteration is totally random. I want a way to save them so if I come back later, or make a map for a game, I can reproduce it. Each configuration is extremely unique, and so I need a fingerprint. There are a couple of ways I can do it, but here's a very simple one.
First, I sort the hexes by their address, then assign 1 for settled and 0 for wilderness. Then I join all those numbers into a long binary string, padded to 400 zeros. For $I=1000$, that looks like this:
0b0000010000000000000010010011000100000000000000001000000000000000000001000000001001110000000000000101000000010000010000000000100000000010101010000100000010010000010001001000000000001000000011100000000000100000000001000100010010100000001101010000110010000000001000000010000000000000000010000100000000001000000000010000000000000000000010000000000100001000001001000100000000101000001011000100110000010000But that's super long! So instead, I'll convert that number into hexadecimal. It's still long, but manageable.
0x400093100008000040270005010400802a840904480080e00200444a0350c802020000840080100000801082440282c4c10I can save this fingerprint for use with this specific hex. When I'm recreating it, I can just pass the seed back to the generator. It's very simple. I think I should try and implement it for the height and river data, but that will require some extra thinking.
June 7, 2019
History XIV: Here I Stand (Summary)
I thought for a bit on how to present a total overview of the system (suggested by Ted), but there are so many moving parts. Still, it's good to sit down and think about it a bit.
This ought to help in keeping things straight. Or perhaps it makes it even more confusing.
It's clear there are several feedback loops: most notably that the city growth rate is affected by the overall tech level of the hegemony. This provides a significant obstacle to small starting cities, but gives a boost to established empires. The loops keep things interesting. In addition, many of these links involve some randomness, which means that things will generally tend in the same direction each time I run the whole simulation, but it's never going to be exactly the same.
Desirability is a value, expressed as a percentage, which describes how desirable a piece of land is for settlement. Each race prefers a different arrangement of terrain and weather. The desirability value will affect how large a settlement can arise in a hex, and also captures the number of resources available there (whether or not they are being totally utilized). Because the resource allotment code adds complexity and time to the history simulation, the desirability is used as an approximation of resources in the battle simulator (since a settlement with access to more physical resources will have an inevitable edge over their adversary). Raw desirability is the desirability in the absence of civilization; it is mixed with infrastructure to obtain a measure of desirability for city expansion, when an existing settlement sends out settlers.
Infrastructure is an integer which describes the effect of settlements on surrounding terrain. Although the Tao only uses elevation to limit the spread of infrastructure, I also include local effects such as forest or desert. I also make infrastructure "flow" downriver easier than upstream. A high enough infrastructure (over 400, for now) changes a forested hex into plains or grassland, depending on the local climate (which is a feedback element encouraging a more efficient infrastructure spread). A higher infrastructure implies a better training mechanism for soldiers. Infrastructure spreads from every settlement in a hegemony and stops at the border.
Hexes with infrastructure but no settlement are the hinterlands; they are prime candidates for future settlements. Since the hinterlands are populated (however sparse), reinforcements can be press-ganged. Generally, however, their population is very low. The rural population of any hex with an infrastructure value is an exponential function of that infrastructure number.
If the effect of a hegemony's capital (measured in % of total infrastructure in a hex) drops too low, and a city's self-generated infrastructure is high enough (100), then a rebellion is possible.
Available resources (which are fed into the market system, not shown) are acquired by cross-referencing the available resources (which is somewhat determined by terrain) with the resource definitions. Certain resources cannot be extracted by low-tech cultures, but may become available as the hegemony grows.
The Long-awaited GitLab. There is no README yet: I've been working on this for two years now, and so the code is a garbled mess in places and cleaner in others. Eventually I'll get around to some housekeeping. Enter at your own risk.
It's clear there are several feedback loops: most notably that the city growth rate is affected by the overall tech level of the hegemony. This provides a significant obstacle to small starting cities, but gives a boost to established empires. The loops keep things interesting. In addition, many of these links involve some randomness, which means that things will generally tend in the same direction each time I run the whole simulation, but it's never going to be exactly the same.
Desirability is a value, expressed as a percentage, which describes how desirable a piece of land is for settlement. Each race prefers a different arrangement of terrain and weather. The desirability value will affect how large a settlement can arise in a hex, and also captures the number of resources available there (whether or not they are being totally utilized). Because the resource allotment code adds complexity and time to the history simulation, the desirability is used as an approximation of resources in the battle simulator (since a settlement with access to more physical resources will have an inevitable edge over their adversary). Raw desirability is the desirability in the absence of civilization; it is mixed with infrastructure to obtain a measure of desirability for city expansion, when an existing settlement sends out settlers.
Infrastructure is an integer which describes the effect of settlements on surrounding terrain. Although the Tao only uses elevation to limit the spread of infrastructure, I also include local effects such as forest or desert. I also make infrastructure "flow" downriver easier than upstream. A high enough infrastructure (over 400, for now) changes a forested hex into plains or grassland, depending on the local climate (which is a feedback element encouraging a more efficient infrastructure spread). A higher infrastructure implies a better training mechanism for soldiers. Infrastructure spreads from every settlement in a hegemony and stops at the border.
Hexes with infrastructure but no settlement are the hinterlands; they are prime candidates for future settlements. Since the hinterlands are populated (however sparse), reinforcements can be press-ganged. Generally, however, their population is very low. The rural population of any hex with an infrastructure value is an exponential function of that infrastructure number.
If the effect of a hegemony's capital (measured in % of total infrastructure in a hex) drops too low, and a city's self-generated infrastructure is high enough (100), then a rebellion is possible.
Available resources (which are fed into the market system, not shown) are acquired by cross-referencing the available resources (which is somewhat determined by terrain) with the resource definitions. Certain resources cannot be extracted by low-tech cultures, but may become available as the hegemony grows.
The Long-awaited GitLab. There is no README yet: I've been working on this for two years now, and so the code is a garbled mess in places and cleaner in others. Eventually I'll get around to some housekeeping. Enter at your own risk.
June 6, 2019
History XIII: Every Manly Heart is Bounding
Not every war is a total war. More often than not, the loser realizes they're fighting a futile war and they surrender. I'll implement a morale score to keep track of this, as suggested by Lance.
Morale goes down when a successful attack is launched against you or a random natural disaster occurs. It goes up when a successful attack is launched by your forces, or you repel an invader. In addition, morale will creep up every year by a small amount.
Because the potential for disaster is very high (0.1% across all cities), and morale is a hegemonic property, morale will tend to drop much quicker than it can rise (absent success in war). This also implies that larger hegemonies will collapse (speaking in morale terms) much sooner than small ones.
If a hegemony's morale (measured from 0-100%) drops below a critical level (10%), it will unconditionally surrender. This is a bit brute force; these surrenders could be very complicated, with vassal states being formed, or a simple exchange of cities, or a total assumption into the conquering kingdom. This latter situation will be enforced, at least until I tackle the vassal state code.
An interesting situation arose where the city of Pawsapa rebelled against the Khare hegemony (a dwarven kingdom of appreciable size) and then destroyed several cities and conquered others, eventually forcing the outlying settlements to declare fealty to Pawsapa instead of Khare. Vieskhare (the founding city) had been established nearly 2600 years before, but a series of natural disasters left her vulnerable to rebellion. A sad story (if you're a Kharen nationalist).
There's also a bug where a large city which surrenders will immediately trigger the secession code and rebel again, forming a new hegemony with a full morale (albeit usually giving up a few cities). It might be a feature instead...
I'm sure I'll continue to tweak the exact values, but the mechanism is at least in place.
Morale goes down when a successful attack is launched against you or a random natural disaster occurs. It goes up when a successful attack is launched by your forces, or you repel an invader. In addition, morale will creep up every year by a small amount.
Because the potential for disaster is very high (0.1% across all cities), and morale is a hegemonic property, morale will tend to drop much quicker than it can rise (absent success in war). This also implies that larger hegemonies will collapse (speaking in morale terms) much sooner than small ones.
If a hegemony's morale (measured from 0-100%) drops below a critical level (10%), it will unconditionally surrender. This is a bit brute force; these surrenders could be very complicated, with vassal states being formed, or a simple exchange of cities, or a total assumption into the conquering kingdom. This latter situation will be enforced, at least until I tackle the vassal state code.
An interesting situation arose where the city of Pawsapa rebelled against the Khare hegemony (a dwarven kingdom of appreciable size) and then destroyed several cities and conquered others, eventually forcing the outlying settlements to declare fealty to Pawsapa instead of Khare. Vieskhare (the founding city) had been established nearly 2600 years before, but a series of natural disasters left her vulnerable to rebellion. A sad story (if you're a Kharen nationalist).
There's also a bug where a large city which surrenders will immediately trigger the secession code and rebel again, forming a new hegemony with a full morale (albeit usually giving up a few cities). It might be a feature instead...
I'm sure I'll continue to tweak the exact values, but the mechanism is at least in place.
Subscribe to:
Posts (Atom)